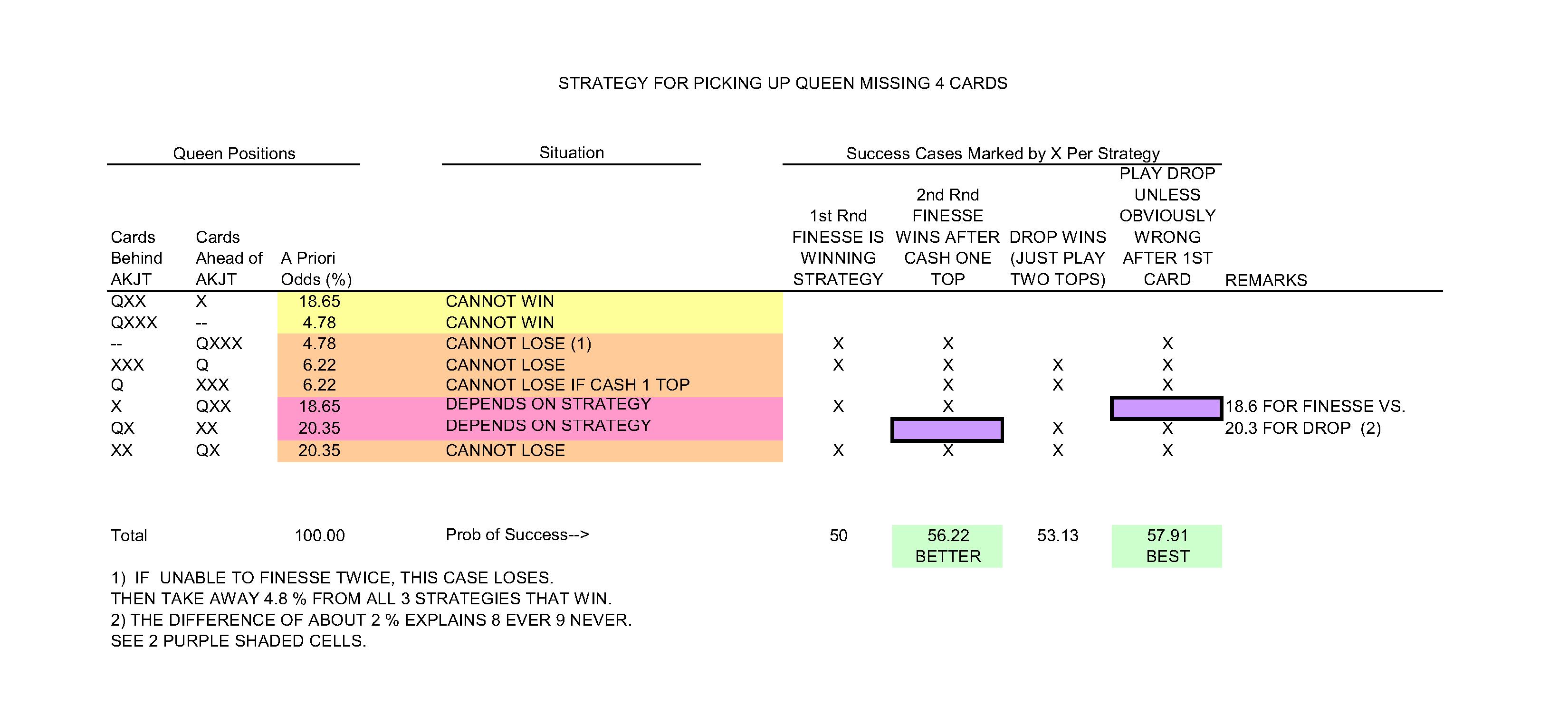
Most players know the “8-ever, 9 never” rule for finding the missing queen, playing a nine-card suit. The image below shows why this rule works. (Click to expand. Type Esc to return, or click the “x” in the upper right corner.)
The odds of success range from about 50% to about 58% for the four strategies. The two best options require playing one top honor and then leading up toward the remaining top honor. The finesse and the drop strategies are less than 2% apart in their original odds of success. However, assuming that you have now seen all three small cards, the current odds have become 12 to 11 for the drop. The difference in present (i.e. updated) probability is 4 % or (1/23). You arrive at this by taking 20.35% vs 18.65% for the two remaining original cases. The current probabilities are
.2035/(.2035+.1865) =.522 (or 12/23) and
.1865/(.2035+.1865) =.478 (or 11/23) .
The finesse at this moment is no longer quite a 50% proposition even though it rated as 56% when you began. Perhaps you wonder where the number 23 came from in the odds.
The “principle” of “vacant places,” or sometimes “vacant spaces,” says that the odds of finding a single particular card are proportional to the number of “vacant spaces” in each concealed hand. Each of those hands start with 13 cards. From 13, you subtract the number of cards in each suit for which the distribution is completely known. In the key suit, when you are down to the missing honor, having located all the other cards, you can subtract those other cards from the concealed hands.
At the decision point, you have seen all the missing spot cards in the key suit. This tells you that the number of vacant places is 13-2=11 in the hand in front of your honor and 13-1=12 behind your honor, so it is better to play for the drop. Suppose you play several cards in other suits before you tackle the key suit. If you do not learn any complete distributions of other suits, you still use 13-2 and 13-1 at the decision point.
Suppose the opponent behind your honors has made an overcall, and his partner has raised. You infer that the suit suit is divided 5-3, with the five cards behind your honors. At the decision point the number of vacant places in front of your honor is 13-2-3 = 8. Behind your honor the number of vacant places is 13-1-5 = 7. This tells you that the odds now favor the finesse by 8 to 7, or about 6.7%. Often a preemptive bid will shift the odds in favor of a finesse.
When considering vacant spaces, you cannot include suits for which you have seen some, but not all cards played. You must know (or choose to assume) the complete distribution of the suits you include. In the key suit, having seen all the spot cards, you can imagine that they constitute a “fifth suit.” for which you know the distribution.
Knowing the complete distribution of one or more side suits in which the defender behind your key-suit honors holds a total of two more cards than his partner tips the balance in favor of the finesse at the final decision point. This assumes you have no other reason to place the missing queen with the opponent holding the 5-carder.